What could be more straightforward than the confidence interval? I compute the mean shoe size of a random sample of first-graders and surround it by whiskers that are roughly twice the standard error of that mean. Presumably I can now have 95% confidence that the “true” value of first-graders’ shoe size, in the population at large, is within the interval defined by the whiskers?

Actually, no. Appearances can be deceptive.

Even though this interpretation appears natural and intuitive, and even though it is advocated by some researchers, it rests on a fundamental fallacy and is therefore false.

A recent article in Psychonomic Bulletin & Review by Richard Morey and colleagues provides an in-depth analysis of confidence intervals and the common fallacies of interpretation. Before we examine the details of their argument, consider the following statements about an hypothetical 95% confidence interval that ranges from 0.1 to 0.4. Simply pick all the ones from the list that you think are correct:

1. The probability that the true mean is greater than 0 is at least 95%.
2. The probability that the true mean equals 0 is smaller than 5%.
3. The “null hypothesis” that the true mean equals 0 is likely to be incorrect.
4. There is a 95% probability that the true mean lies between 0.1 and 0.4.
5. We can be 95% confident that the true mean lies between 0.1 and 0.4.
6. If we were to repeat the experiment over and over, then 95% of the time the true mean falls between 0.1 and 0.4.

It should have been easy to identify number 5 as false because I already mentioned that fallacy earlier. But what about the others?

It turns out that they are all false.

If you thought number 6 was true, then that’s because it is worded in a manner that on a quick skim may appear correct. The correct version is: “If we were to repeat the experiment over and over, then 95% of the time the 95% confidence interval would cover the true value of the mean.”

This seemingly subtle difference between what is correct and what is wrong lies at the heart of the work by Morey and colleagues. The key confusion underlying many misconceptions of the confidence interval lies in muddling the distinction between what is known before observing the data and what is known afterwards. What we know before we collect data is that the confidence interval—whatever it may turn out to be—has a 95% chance of containing the true value. What we know after we’ve collected the data is, err…. not much: conventional frequentist theory says nothing about after-the-fact—that is, “posterior”—probabilities.

This basic limitation of frequentist statistics is more readily explained in the context of hypothesis testing. If we run a statistical test on our experimental data and obtain a small p-value, let’s say .01, then it is tempting to conclude that the probability of this outcome being due to chance is 1%. However, this inference would be invalid: A p-value tells us about the probability of observing a given outcome (or something more extreme) if chance were the only factor at play (the conditional probability P(D|H0))—but that is not the same as the probability that an observed event was due to chance. To infer the probability of chance being at work, we must also consider the probability that the observed data would have been obtained when the null hypothesis is false. That probability is never considered in conventional hypothesis testing, but it can have substantial effects on our inferences: If that alternative probability is also low, then a small p-value may not be associated with a small probability of chance having caused the observed effect. If neither chance nor the presence of an effect render an observed outcome likely, then that outcome does not permit a strong inference about the presence (or absence) of chance no matter how small the p-value. This interpretative subtlety is not only important when evaluating the outcomes of studies but it can also have particularly dramatic—and tragic—ramifications in jurisprudence.

In the same way that a small p-value does not permit an inference about whether chance was the sole determinant of an observed outcome, an observed confidence interval typically does not permit any inference about the value of the underlying population parameter.

The fact that frequentist statistics do not permit inferences from an observed outcome to the true state of the world is a serious barrier to scientific reasoning. After all, it is our core business to infer the state of the world from the data we observe—and yet, with conventional frequentist statistics this inference is never organic and often wrong. Given how badly we need to make such inferences, it is perhaps not surprising that numerous fallacies about confidence intervals have become commonplace.

Morey and colleagues survey those fallacies, and it is worth highlighting a few of them this week. Let me remind you that they are fallacies, no matter how desirable and convincing they appear at first glance.

Let’s first examine exactly why it is fallacious to conclude from an X% confidence interval that there is an X% chance that the true value lies within the observed interval. To explain this, Morey and colleagues provide a nifty online simulation. You may want to open this simulation now in a new tab and move it to the side so you can continue reading while also following through with the simulation. For those who don’t want to do that, I am reproducing the crucial figure below.

The situation is this: A 10-meter-long submarine sits disabled at the bottom of the ocean. The submarine has a rescue hatch exactly halfway along its length. You get one attempt at dropping a rescue line in the right place. You do not know where the vessel is, but you can observe pairs of air bubbles that rise to the surface, and you know from experience that they can form anywhere along the craft’s length, independently, with equal probability.

If that is difficult to decode, simply think of the problem as a uniform distribution that is known to range from m-5 to m+5, where m is the location of the rescue hatch (i.e., the mean) that you are trying to infer from two independent samples.

How?

Simple—by computing a confidence interval around the sample mean. For present purposes, we use 50% as the width of our confidence interval, and we exploit our knowledge of the sampling distribution of the mean to compute the width. The figure below presents various confidence intervals for two possible observed outcomes: On the left (Panel A), two bubbles have been observed close together, and on the right (B) they have been observed far apart. I have highlighted the row that should concern us now, which corresponds to a frequentist 50% interval based on the sampling distribution of the mean. You can ignore the other rows for now.

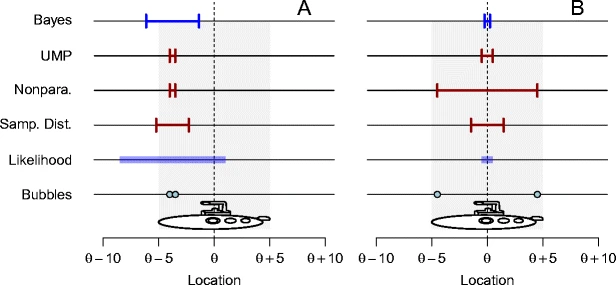
The figure shows what you would expect: In both panels, the confidence intervals are centered around the mean location of the two bubbles.

If you use the online simulation to draw 1,000 samples, then you will find that indeed, around 500 of those 50% confidence intervals will contain the location of the rescue hatch, whereas the remainder do not.

But does this mean you can infer the probability with which the hatch is contained in a given observed confidence interval? No—because those probabilities actually differ considerably between the two panels. This difference arises because the distance between bubbles itself tells us something, and this information is lost in conventional frequentist analyses: Consider an extreme case in which the two bubbles surfaced in the same location. This tells you very little because the escape hatch could be anywhere within 5 m of either side of the bubbles. Now consider another case, in which the two bubbles are exactly 10 m apart. This tells you everything, because the only place where the hatch can possibly be is exactly midway between the two bubbles.

The figure above presents attenuated versions of those two extreme cases. Crucially, the 50% confidence interval in Panel B is the same width as it is in Panel A, even though it is nearly certain to contain the location of the hatch.

It follows that it is inappropriate to assign any kind of confidence to confidence intervals. And this is just the first fallacy. Stay tuned for more later this week.

Reference for the paper mentioned in this post:

Morey, R. D., Hoekstra, R., Rouder, J. N., Lee, M. D., & Wagenmakers, E.-J. (2015). The Fallacy of Placing Confidence in Confidence Intervals. Psychonomic Bulletin & Review, doi: 10.3758/s13423-015-0947-8.