In yesterday’s post, I showed that conventional frequentist confidence intervals are far from straightforward and often do not permit the inference one wants to make. Typically, we would like to use confidence intervals to infer something about a population parameter: if we have a 95% confidence interval, we would like to conclude that there is a 95% chance that the true value lies within the observed interval.
Unfortunately, as shown in a recent article in Psychonomic Bulletin & Review by Richard Morey and colleagues, this inference is usually not warranted. A simple way to illustrate this is to envisage a situation in which we sample N observations from a normal distribution with known (population) variance. In that situation, because the variance is known, we are entitled to use z-statistics to compute the 95% confidence interval around the mean of our N observations. But there is also nothing to prevent us from computing the 95% confidence interval based on the t-statistic—after all, the sample variance s2 is an unbiased estimator of σ2, the population variance. Now here is the problem: for any sample size N < ∞, the confidence interval based on z will be smaller than that based on t. It follows that if both intervals contain the population mean with 95% confidence—as we postulate by our desired interpretation of confidence intervals—then we must simultaneously have zero confidence that the population mean could lie between the boundaries of the z and the t-intervals. (Because the smaller z-interval that sits within the t-interval has already “soaked up” all of the 95%.)
If you find this weird, that’s because it is. It’s not just weird, it’s absurd, and it arises from the troubling properties of the frequentist confidence interval that do not permit the inferences we would intuitively like to make.
Here is another, possibly even more troubling attribute: Under some circumstances, the more we could know about the desired parameter, the less confidence will be implied by the confidence interval. More potential knowledge translates into greater uncertainty.
Not good.
To illustrate this “precision fallacy”, let’s again consider the submarine example used by Morey and colleagues in their article. Recall that a 10-meter-long submarine sits disabled at the bottom of the ocean. The submarine has a rescue hatch exactly halfway along its length and your job is to locate that hatch to rescue the crew. You do not know where the vessel is, but you can observe pairs of air bubbles that rise to the surface. You know from experience that the bubbles can form anywhere along the craft’s length, independently, with equal probability.
This situation is again illustrated in the figure below of the online simulation provided by Morey and colleagues, which displays a variety of 50% (not 95%) confidence intervals:
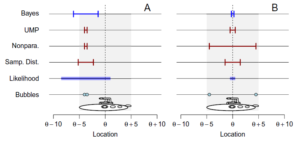
In yesterday’s post, I showed how the conventional confidence interval can severely underestimate the probability that the interval covers the true parameter. This is because in panel B on the right, we can be quite certain where the hatch is: the two bubbles are nearly 10 meters apart, and given that the submarine is 10 meters long with the hatch exactly in the middle, the two bubbles tell us a lot. (If this isn’t clear, revisit yesterday’s post.)
Today I show that the conventional confidence interval can be even more misleading, by returning seemingly less information about a parameter when we know more. This is known as the “precision fallacy” and arises because the conventional interval does not take into account the likelihood; that is, it ignores the information provided by the joint probability density of the observed data for all possible values of the parameter of interest (in this case, the hatch location).
In the figure above, non-zero values of the likelihood are shown by the thick blue bar. Wherever there is no bar, the likelihood is zero. We can determine the likelihood from the constraints embodied in the problem: in the left panel (A), the two bubbles are close together and hence the hatch could be at most nearly 5 meters away in either direction (because if the two bubbles were on top of each other and emerged from the very tip of the submarine, the hatch would be exactly 5 m either way—it couldn’t be any further away because it’s in the middle of a 10 m vessel). In the right panel (B), as we have already noted, the bubbles are so far apart that the hatch has to be in the middle, with relatively little uncertainty (if the bubbles emerged exactly 10 m apart, there would be zero uncertainty—you can verify this using the simulation.)
So what do conventional confidence interval do with this valuable information?
Nothing.
Instead, they give the appearance of confidence by considering the variance in the sample. Intuition—and widespread practice—suggests that the smaller the variance, the more precise the estimate of the parameter, and hence the greater our confidence in the true value of the parameter should be.
Unfortunately, the reverse is true in the current situation. This is because the “variance” among the two bubbles is minimal in panel A but maximal in panel B. Hence the appearance of precision is greater on the left than the right—even though we have nearly perfect knowledge available in the right-hand panel.
This is illustrated in the row labeled “Nonpara.” in the figure above, which also happens to be the conventional frequentist interval computed with the t-statistic. In other words, this is your textbook case where you compute the mean (of the two bubbles), and then the standard error of the mean according to s/√N (where N=2 here). The width of the confidence interval is thus directly proportional to the distance between the bubbles: large on the right and tiny on the left.
The implied presumed “precision” in panel A is entirely chimerical: the confidence interval is nice and tight but is cruising right past the true value. Conversely, in panel B we seem quite uncertain when in fact we could know pretty much exactly where the hatch is. (There is a nuance here which renders the use of s/√N questionable, and which explains why the row is called “Nonpara.” For expository purposes I am ignoring this infelicity.)
In summary: conventional frequentist confidence intervals tacitly convey images of precision (or lack thereof) that can run completely counter to the actual knowledge that is available in a given situation. Fortunately, therefore, the people who looked for the black box of Air France Flight 447 did not rely on frequentist statistics.
They instead relied on Bayesian search theory. As did the U.S. Navy when it located the nuclear submarine USS Scorpion.
The idea of Bayesian search theory is the same as for any other Bayesian statistical inference: You formulate as many reasonable hypotheses as possible (in the above figure, this is the space of possible locations of the hatch). You then construct the likelihood (the joint probability density of the observed data for all possible locations of the hatch). Finally, you infer the probability distribution of the location of the hatch from the likelihood and the presumed prior distribution of locations. In the case of the figure above, this simplifies to half the width of the range of non-zero likelihoods (because we are concerned with 50% confidence intervals and we assume a uniform prior).
Accordingly, in the figure above, the top row shows 50% Bayesian credible intervals that are half the width of the blue bars indicating the nonzero likelihoods. They are narrow in panel B and wide in panel A, as they should be.
It is for this reason that they are called credible intervals—because they are just that: credible.
Reference for the paper mentioned in this post:
Morey, R. D., Hoekstra, R., Rouder, J. N., Lee, M. D., & Wagenmakers, E.-J. (2015). The Fallacy of Placing Confidence in Confidence Intervals. Psychonomic Bulletin & Review, doi: 10.3758/s13423-015-0947-8.

3 Comments