People are capable of inferring many attributes of an object by wielding it. Pick up a hammer and you can get a fairly good idea of its length, width, and shape (an ability that is known as exteroception). You will also acquire information about the orientation of the hammer in your hand (exproprioception), and your hand’s location on the hammer (proexteroception). This is all assuming, of course, that the object itself does not change as you wield it. All bets are off when the object is dynamic and changes shape in your hand.
Key to our exteroceptive ability is the rotational inertia exhibited by an object. That inertia increases with the distance between the axis of rotation and the concentration of mass of the object: grab a hammer by the head and it is much easier to flick around than when you hold it by the handle. Same hammer, same overall weight, but very different inertia depending on where the mass is concentrated relative to the axis of rotation.
There is, however, another variable that affects rotational inertia and that is commonly ignored because we take it for granted. That variable is the medium in which the object is wielded: a lightsaber in the vacuum of outer space behaves differently from a hammer swung through air. That hammer, in turn, will feel very differently when wielded under water or in some other viscous substance.
It turns out that the medium interacts with the specific gravity of an object to determine its rotational inertia in a rather complex pattern. The specific gravity of a hammer made of balsa wood is low (it’s 0.2 with reference to water) whereas a hammer made of gold has a specific gravity that is about 100 times greater (20 with reference to water). The figure below shows the implications:
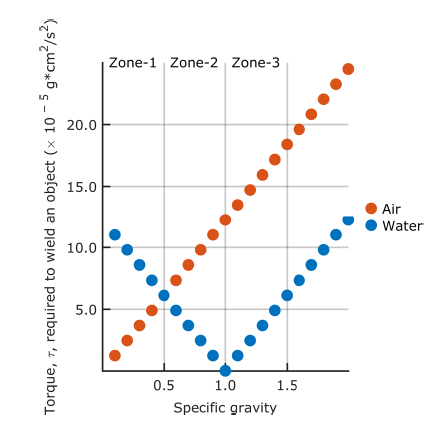
The figure shows that the denser an object is, the greater is the torque that is required to move it in air (red dots). Swinging a balsa hammer is just a lot easier than swinging a gold hammer. Under water (blue dots), the situation is quite different: anything lighter than water (specific gravity < 1; left half of the figure above) floats, and the more an object wants to float, the more that force must be counteracted by the human who is wielding the object.
The physics of rotational inertia give rise to an interesting psychological question: are people sensitive to the density of the medium in which an object is wielded? If they do not know the medium, can they nonetheless infer the length of an object from wielding it?
A recent article in the Psychonomic Society’s journal Attention, Perception, and Psychophysics addressed these questions. Researchers Madhur Mangalam, Sophie Barton, Jeffrey Wagman, Dorothy Fragasz, and Karl Newell devised a clever apparatus, shown in the figure below, that enabled participants to wield unknown objects in an unknown medium and estimate their length from that dynamic interaction alone:

The participants wore a glove on their right hand, and on each trial they were handed an object by the experiment and then wielded it about their wrist and reported its perceived length by sliding a pointer on a response scale. There were no restrictions on the wielding motion except that participants were instructed to avoid hitting the walls of a container with the object.
The stimulus objects were rods of varying lengths that were made of, pine wood, maple wood, or aluminium. The three materials covered the crucial range of specific gravity (see the first figure above), with values ranging from 0.86 (pine) to 3.69 (aluminium). To obscure the composition of the objects from participants, one end was covered in a rubber grip. The distribution of mass was altered by placing rings at various distances from the grip.
The analysis revealed several strong effects: perceived length increased with specific gravity of an object, and it increased with the distance of the concentration of mass from the hand (i.e., the location of the rings on the rod). Intriguingly, there was no effect of medium: the average perceived length in air was virtually identical to perceived lengths in water.
To further characterize people’s length judgments, Mangalam and colleagues resorted to a mathematical analysis of the hand-object system that is summarized in the next figure.
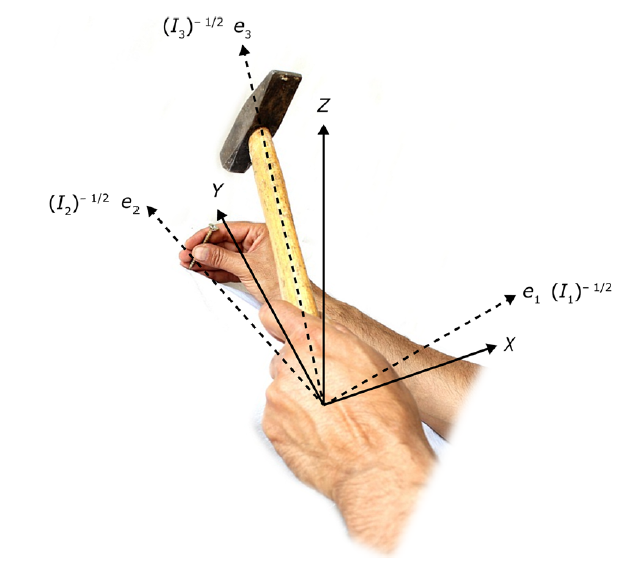
The three dashed lines in the figure describe the symmetry axes of the hand-object system and specify the orientation of the object. The parameters I1, I2, and I3 (actually they are eigenvalues of the inertia tensor) describe the resistance of an object to rotation about the associated symmetry axes. Mangalam and colleagues computed the values of I1 and I3 for all stimuli (I2 played no role in this instance because the rods were symmetrical about this axis) and used those physical values to predict people’s length judgments. The figure below shows the results.
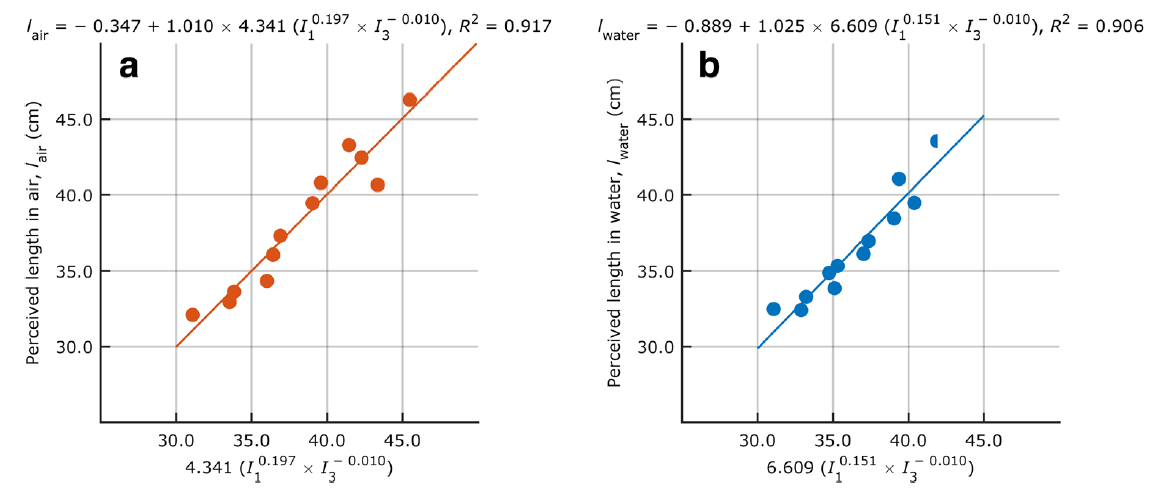
It is quite clear that people’s judgments were described very well as a function of the physical inertia of the objects. Remarkably, the functions were nearly identical for air and water—predicting the results for air from the parameters estimated for water (and vice versa) yielded nearly identical values of R2. Mangalam and colleagues concluded that “the haptic information for perception of length by dynamic touch is invariant across changes in the medium.”
How can the perceived length of a wielded object not be affected by the medium? Surely it’s easier to swing a hammer through air than water, so why would one’s length judgment not be affected by that difference?
The answer lies in the fact that wielding of an object is a cyclical motion—you swing a hammer up and down (and again and again). Cyclic movements permit the extraction of rotational inertia independent of the torque that is required to move the object. Specifically, to initiate a rotation one must overcome not just the rotational inertia of an object, but also its weight and the drag acting on it during the motion through the medium. At the end of the arc, to initiate the movement in the opposite direction, one must again overcome the rotational inertia of the object, but this is now aided by the weight of the object and the drag acting on it while still in motion. Put the two together, and weight and drag are cancelled out in the cyclic motion and all that is left is the torque required to overcome an object’s rotational inertia.
The fact that the human information processing system can isolate rotational inertia from all the other physical variables impacting an object’s motion may explain why Luke Skywalker can fight with Darth Vader and live to tell the tale.
Psychonomics article highlighted in this post:
Mangalam, M., Barton, S. A., Wagman, J. B., Fragaszy, D. M., & Newell, K. M. (2017). Perception of the length of an object through dynamic touch is invariant across changes in the medium. Attention, Perception, & Psychophysics, 79, 2499-2509. DOI: 10.3758/s13414-017-1403-9.

