When we talk about statistical modeling, we often encounter the concept of “degrees of freedom.” Remember? It’s the n-1 in t[n-1] or the [1] in χ2[1]. In our off-the-shelf statistical procedures, the degrees of freedom refers to the information content of some statistical construct. It can loosely be thought of as the number of independent values that are needed to describe the construct without loss of information.
We can talk about the degrees of freedom of a data set (usually, the number of observations), about the degrees of freedom in a model (usually, the number of parameters) and the degrees of freedom error (usually, the difference).
As an example, consider the data set {1, 1, 2, 5, 6}. This set has five independent elements and so (assuming the order of elements does not matter) it has five degrees of freedom. However, we could describe the same set, without loss of information, by saying the mean is 3 and four of its elements are {1, 1, 2, 5}. The fifth element can be derived. The degrees of freedom have been partitioned into one {for the mean} and four {for the remaining elements}. For a slightly more sophisticated example, consider that we could express the same set again by its mean, 3, and four deviations of the mean {-2, -2, -1, 2}. Knowing that deviations from the mean will sum to zero, the final deviation (which is 3) is redundant with respect to what is already known. When we are fitting linear models, we always end up sacrificing some of the data’s degrees of freedom to turn them into more interpretable model parameters such as means, intercepts, slopes, and so on.
However, it is not always that simple. In the context of classical hypothesis testing, degrees of freedom can appear in more subtle and unexpected ways. It is not always recognized that researchers who analyze a new data set, and implicitly traverse a potentially tall decision tree of choices on the way, possess a number of degrees of freedom also. For example, a researcher analyzing reaction time data might choose to discard fast responses below 200 ms, or below 250 or 300 ms, or they might not discard fast responses at all. Independently, they might discard slow responses above 2000 ms, 3000 ms, or any number that seems reasonable. Then, they might apply a variance stabilizing transformation to the reaction times—perhaps a logarithmic transform, or the inverse. Alternatively, they might choose to fit a process model, such a diffusion model, a linear ballistic accumulator, or a race model.
The possible choices are legion. These “researcher degrees of freedom” (RDOF) have been a topic of some discussion since the term was coined by Simmons and colleagues.
Readers of empirical journal articles ignore RDOF at their own peril. In the presence of an unknown number of researcher degrees of freedom, inferential statistics such as the p-value are uninterpretable, no matter how well the degrees of freedom associated with the t or F statistic are known. After all, p is meant to give the conditional probability of obtaining data of the observed extremity, assuming the truth of a well-specified null hypothesis. However, researchers who opportunistically change (for example) their outlier exclusion rules, the dependent or independent variable to use, or the null hypothesis to challenge, consequently also change the probability with which some extreme data will be observed. Thus, the reported p-value no longer corresponds to the nominal conditional probability.
The extent to which unacknowledged RDOF can affect scientific conclusions was illustrated in dramatic fashion by in a recent collaborative project. In this project, 29 teams of analysts were given the same data set and asked to answer a fairly straightforward empirical question: Are soccer referees more likely to give red cards to dark-skin-toned players than to light-skin-toned players? The analysts were given data on 146,028 player-referee dyads and how often each dyad had resulted in a red card. In addition, they were given a range of potential independent variables, which the teams could choose to include in their analysis (or not). Of the 29 teams, 20 found a statistically significant bias against dark-skin-toned players, while 9 teams did not.
In the absence of a ground truth, it’s hard to say whether there were 20 groups who generated a false alarm, or 9 who generated a miss—and that’s not the right question here anyway. What is clear is that, if you make one justifiable set of statistical assumptions, the conclusion goes one way, whereas under a different justifiable set of assumptions, it goes another way. Since it is not clear which approach and which set of assumptions is better, whether you now believe in the effect is a matter of scientific judgment. Statistical inference is unavoidably a subjective endeavor, even in the case of a fairly workaday statistical scenario.
Even when analysts are not given broad freedoms in which predictors to choose, the specific choice of model, ancillary assumptions, or inferential method, might still affect the ultimate conclusions.
In a recent article in the Psychonomic Society’s Psychonomic Bulletin & Review by Gilles Dutilh and roughly 27 co-authors (disclosure: I am one of them), analysts were not given a set of possible covariates—only the reaction time and accuracy data in 14 “pseudo-experiments.” Data for the pseudo-experiments was generated using a real data set in which participants responded to random dot motion trials under a variety of instruction conditions; these data were then rearranged pairwise, yielding 14 data sets with two conditions each. The 14 data sets mimicked experiments in which researchers manipulated the difficulty of the task, the caution of the participant, the bias towards one or the other response, or the non-decisional reaction time component.
Astute readers will recognize these data features as classical parameters of cognitive process models such as the diffusion model and other sequential sampling models of reaction time. Indeed, this was how these data sets were presented to researchers, together with a challenge to use a cognitive model in order to identify which of these features had been targeted for experimental manipulation.
Seventeen teams were found willing to contribute their best analysis of these data sets and asked to ply the subtle science and exact art of model-based inference.
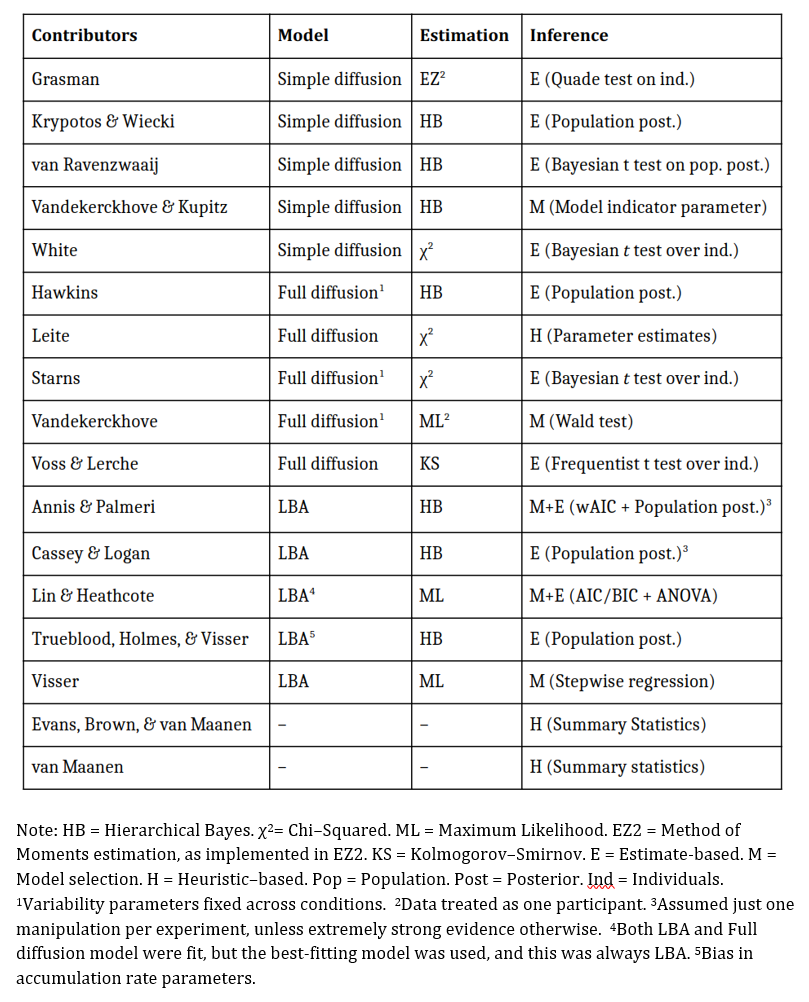
Two major conclusions followed from this exercise. First, in the words of Dutilh and colleagues: “The first result worthy of mention is that the 17 teams of contributors utilized 17 unique procedures for drawing their inferences. That is, despite all attempting to solve the same problem, no two groups chose identical approaches. This result highlights the garden of forking paths that cognitive modelers face.”
Indeed! A quick glance at the table below (adapted from Table 3 in the paper) reveals that, not only are all 17 models unique, they all differ in key components — no two approaches are, say, identical but for some numerical assumptions. All use a unique combination of model, constraints, and inferential method. Against this backdrop, the second observation is perhaps surprising. Comparing the conclusions submitted by the 17 teams, Dutilh et al. write: “in most cases there is a clear majority conclusion. Such agreement between methods is reassuring, given the issue of RDOF. That is, regardless of the choice of model, estimation method, or approach to inference, the conclusions drawn from the models tend to overlap substantially.” The impression here is that, at least within this context, conclusions from model-based analyses are more robust to the arbitrary decisions made by the researchers.
We can probably agree that projects of the type conducted by Silberzahn, Dutilh, and colleagues, with all the effort they require, are heroic. The question is, why were they necessary? Are RDOF an acute issue? Are they a recent development? The answer to the last question is simply “no.” It is well known that researchers regularly engage in “statistical fishing” — the common phrase used to describe the process of gradually exploring the degrees of freedom in an analysis. The practice is far from new. Why the recent interest, then? The description and illustration of the power of RDOFs dovetails with the movement towards greater openness and transparency in science.
Since these degrees of freedom are difficult to quantify, the agreed-upon strategy to minimize their influence is to reduce RDOF as much as possible from the outset. For example, researchers who lock in their data analysis plan before seeing the data have removed all of their RDOF. Such locking in can occur as part of an online pre-registration, or during the submission or a registered report, or the analysis could be devised by a statistician who is blind to the actual outcomes. These mechanisms all serve to mitigate the deleterious influence of RDOF and so, to safeguard the correct interpretation of p-values.
Psychonomics article focused on in this post:
Dutilh, G., Annis, J., Brown, S. D., Cassey, P., Evans, N. J., Grasman, R. P., … & Kupitz, C. N. (2018). The quality of response time data inference: A blinded, collaborative assessment of the validity of cognitive models. Psychonomic Bulletin & Review, 1-19. DOI: 10.3758/s13423-017-1417-2.
