Yogi Berra once famously said that “You can observe a lot by watching”. Yogi Berra observed and said a lot of things, but this line has a lot going for it. The idea that information can be gathered by “just looking” entered statistics many decades ago. For example, John Tukey, one of the 20th century’s greatest statisticians, stated that his favorite part of analyzing data was “taking boring flat data and bringing it to life through visualization.”
It is perhaps unsurprising that some graphs have become iconic symbols of entire scientific fields. For example, modern astronomy would be nearly unthinkable without the Hertzsprung-Russell diagram, which beautifully illustrates stellar evolution. The diagram itself has even attracted a peer-reviewed article in the American Statistician that reviews its beauty and importance. The figure below is taken from that article:
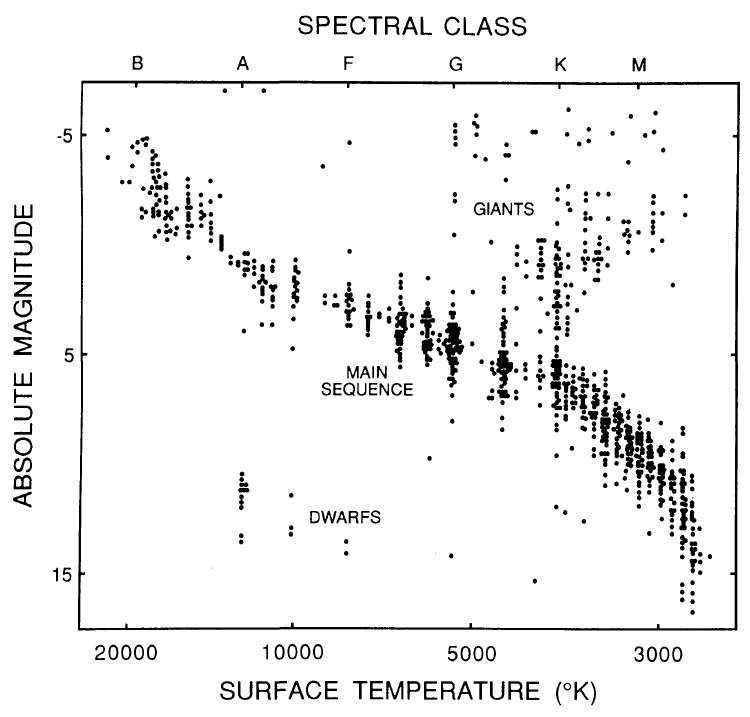
The diagram shows the main sequence of stars, whose absolute magnitude (i.e., visual impact corrected for distance) declines with surface temperature. But the main sequence does not tell the whole story: there is a separate cluster of stars, known as “giants” that are hot and bright and do not fall on the main sequence.
It turns out that the diagram describes the evolution of stars over time: this video provides an animation of what we know about stellar evolution.
[youtube https://www.youtube.com/watch?v=NvEaLlVd5iw]
Much of what we know about that evolution has been inferred from the Hertzsprung-Russel diagram.
In other cases, graphs have had an immediate visceral impact and have stimulated intense public debate. Consider the graph below, which shows global temperatures during the past 1,000 years.


The visual impact of those data is difficult to escape—and this may be one reason why this graph, known as the “hockey stick” has evoked so many attempts to deny or question the data it shows.
In light of the scientific and public importance of graphs, it is not surprising that researchers have begun to address the cognitive processes that are involved in the comprehension of graphs.
A recent article in the Psychonomic Bulletin & Review focused on the specific issue of how people perceive correlations in scatterplots. Although correlation statistics, such as r (the correlation coefficient) can be readily computed, perceptual tasks involving correlations in scatterplots are an ideal testbed to examine how we process statistical information: On the one hand, it is known that estimation of r appears to be a simple visual process. On the other, scatterplots offer sufficient complexity to raise interesting questions about the complexity of information processing involved.
Researcher Ron Rensink conducted 4 experiments that explored the details of how we perceive correlations. In each experiment, observers had to perform two tasks: they had to discriminate between correlations by deciding which of two side-by-side scatterplots was more correlated. Participants also had to estimate the magnitude of correlations, by adjusting the correlation in one plot until its perceived correlation was exactly halfway between those of two reference plots shown on the screen.
Stimuli for the discrimination task are shown in the figure below:

As a participant you would be asked to choose the plot that appeared more correlated. This choice probably appears easy: But it’s not your expertise that makes the task easy because it turns out that—perhaps surprisingly—the ability to process correlations is largely independent of the statistical expertise of the observer.
The stimuli for the estimation task are illustrated in the next figure:
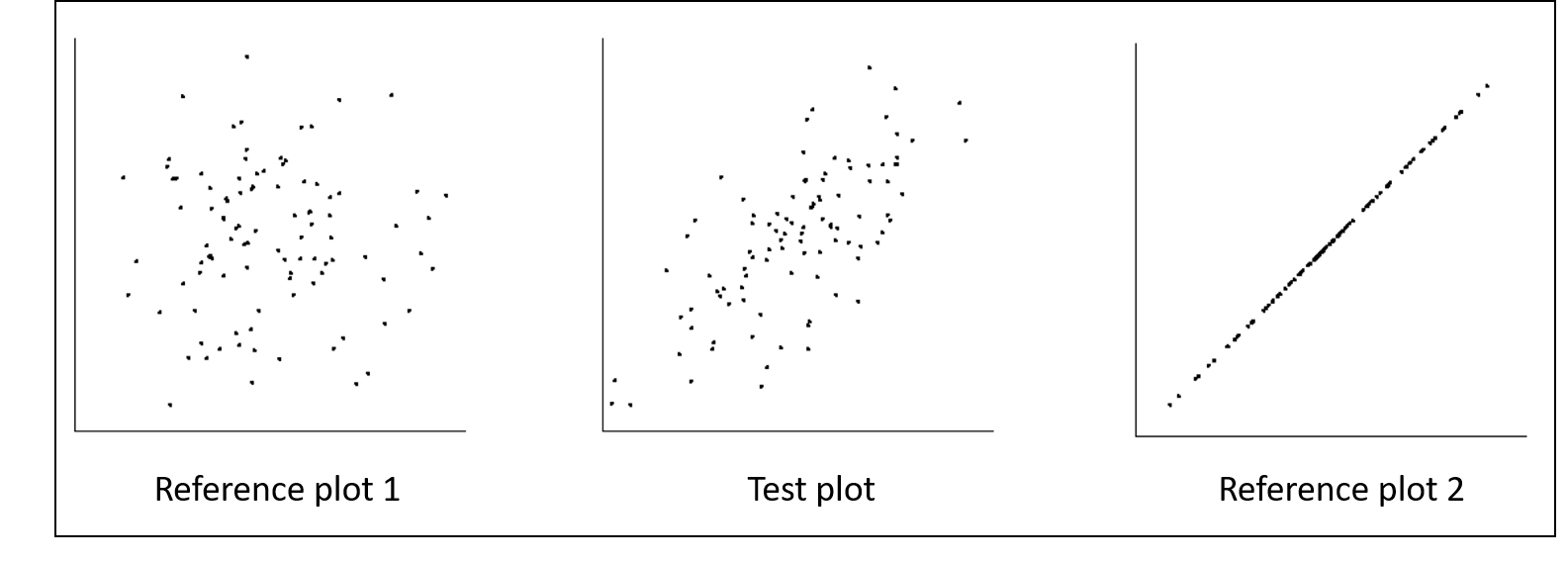
Here your task would be to adjust the test plot in the middle until its perceived correlation was halfway in between the reference plots—to make this a bit more difficult, every time you adjust the point cloud in the middle, all 3 stimuli would be replaced by new samples. That is, the specific points were replaced every time without affecting the correlation of the reference plots.
The results were remarkably consistent across the 4 studies, which varied various aspects of the scatterplots such as their aspect ratio, density (number of points), and so on. The next figure illustrates the results from one of the experiments, in which the point clouds happened to be drawn from a uniform distribution:
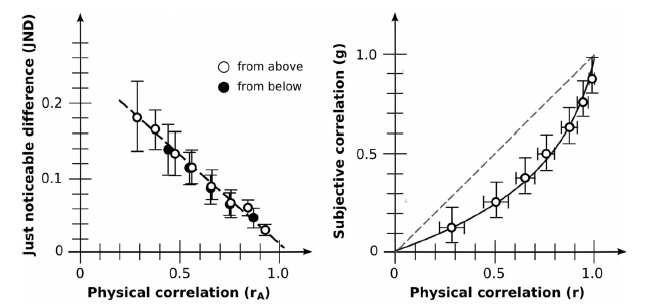
The data look remarkably similar across experiments, so we need not be concerned with those details here.
The panel on the left shows the results from the discrimination task, and the panel on the right contains data from the estimation task. The discrimination data are expressed as the “just noticeable difference” or JND, which refers to the point at which the two correlations were correctly discriminated 75% of the time. The smaller the JND, the greater the discriminability. The estimation data are expressed as the correlation to which the test plot was adjusted, as a function of the true correlation that is halfway between the two reference plots.
In both panels, the physical correlation is plotted on the abscissa (X-axis). The data differ strikingly between panels: whereas discrimination performance is a linear function of physical correlation, such that accuracy increases as the magnitude of the correlations to be compared increases, there is a curvilinear (logarithmic) relationship for the estimation task.
Why do the data take the form they do?
Rensink puts forward three suggestions to explain the data: First, people are thought to infer something quite abstract from the plot. This abstract representation must involve more than just a geometric image of the point cloud because in other experiments, correlation perception has been found to obey the same pattern as in the above figure, even if one of the spatial dimension (i.e., the Y-axis in the scatterplot) is replaced by something entirely different—such as the size of circles or orientation of lines.
Second, people are thought to estimate a probability density function from this abstract representation, whose width is one principal determinant of how correlations are perceived. The figure below shows how a scatterplot maps into this presumed density representation:
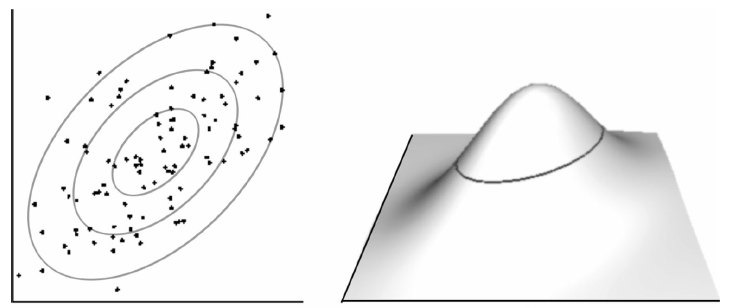
It turns out that the function relating perceived magnitudes to physical correlations can be reproduced from (among other parameters) the presumed width of the three-dimensional density function on the right of this figure.
Finally, Rensink suggests that the reason people rely on the width of a probability distribution is because the visual system can detect the information entropy inherent in the plot, and this quantity is used as a proxy for the correlation. Entropy turns out to be related to the width of the above distribution.
One practical implication of these results is that if people’s perception of scatterplots is based on an abstract probability distribution, then properties other than spatial position—such as color, size, or orientation—may be equally useful for displaying correlations.
Article focused on in this post:
Rensink, R. A. (2016). The nature of correlation perception in scatterplots. Psychonomic Bulletin & Review. DOI: 10.3758/s13423-016-1174-7.
